Table of Contents

This post analyzes transformer models, specifically memory and computation overhead.

Many transformer based models just explain themselves as a model with X-B parameters; I wanted to break it down and look into the model structure how they are stored and used in actual computing hardware.

Many illustrations and analysis are based on the following papers ¹.

Transformer-based Model #

Since Google announed attention and transformer models in 2017 ², MLP and image classification models are rapidly adopting transformer layers. Redrawed from the paper ¹, basic transformer architecture looks like this:

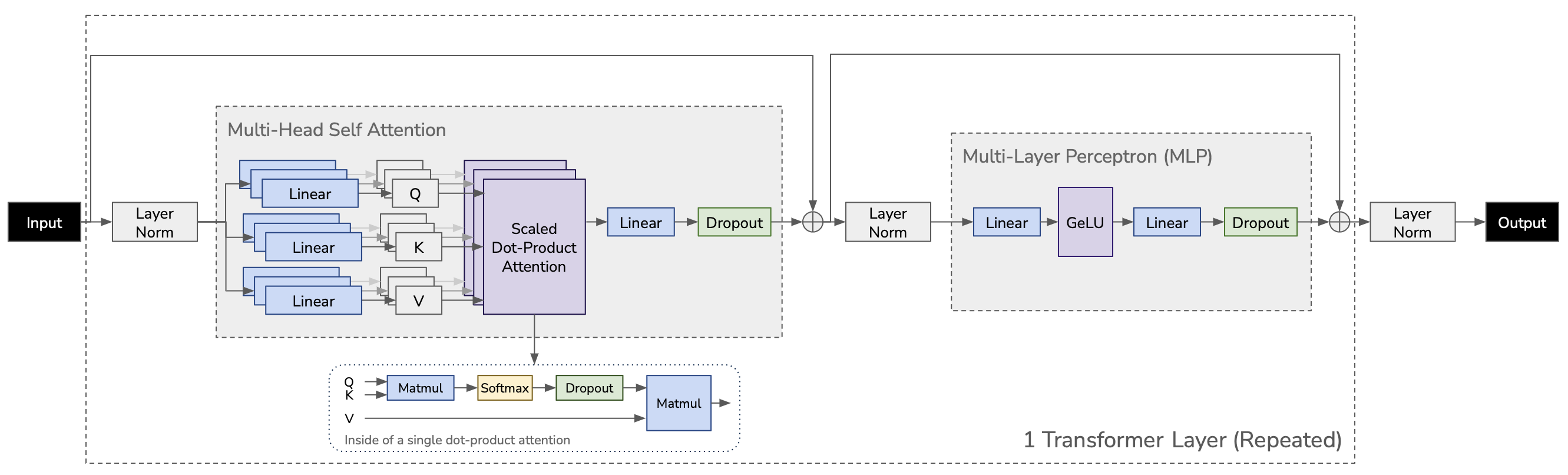
MLP is the same with feed-forward layer in GPT. For more information about GPT specific illustration, refer to this post.

For example, GPT-2 XL has 48 transformer layers, hence has 1.5B parameters ³. But how this number comes out? Which layers in the figure have parameters? And how many memory is actually required to train this model? This is the goal of the post.

Following the paper ¹, I used the following variable names in the rest of the post:

$a$: number of attention heads. (GPT-2 medium: 16)
$b$: number of microbatch. (variable hyperparameter.)
$h$: hidden dimension size. (GPT-2 medium: 1024)
$L$: number of transformer layers. (GPT-2 medium: 24)
$s$: sequence length. (GPT-2 medium: 1024)
$v$: vocabulary size. (GPT-2 medium: 50,257)

The other variables (pipeline parallel size and tensor parallel size) are not used here.

Memory Consumption #

Memory consumption in training can be divided into the following four types:

model: model parameters (weights).
activation: after doing forward pass, the result of computation is stored and reused in backpropagation to calculate weight gradient (Can be discarded and recomputed via activation recomputation, I ignore this technique here).
gradient: calculated during backpropagation. Used to update model parameters.
optimizer state: e.g. Adam optimizer uses internal states to keep gradient momentum. Optimizer state includes such optimizer-specific data.

Model Parameters (or Weights) #

Model parameters are stored in FP16 in mixed precision, so each parameter takes 2 bytes.

From the figure, all linear projection layers have their parameters. I omitted biases and normalization for layers.

To calculate Q, K, and V, $W^Q, W^K, W^V$ are used. Each $W$ has dimension of [$h$, $h$], Total number of parameters is $3h^2L$. Note that this linear projection calculates all Q, K, and V for $a$ attention heads at once.
The result of multiple attentions are concatenated and fed into linear projection (and dropout) before going into MLP. Total number of parameters for linear here is $h^2L$ ([$h$, $h$]).
MLP accepts the outputs from attention ($h$), casts them to $4h$ (here, the linear projection has parameters of [$h, 4h$]), applies GeLU, casts them back to $h$ (this linear projectionh as parameters of [$4h, h$]). In total, we have $8h^2L$ parameters.
Word embeddings and positional encoding: The input of the entire model is calculated from word embeddings and position encoding. Numbers of parameters are $vh$ and $sh$, respectively. See Illustrated GPT-2 for more details.

Total # parameters: $Lh^2(3 + 1 + 8) + vh + sh$. If we focus on each layer, it is $12h^2$.

For instance, GPT-2 medium: $24 * 12 * 1024^2 + 50257 * 1024 + 1024^2 = 354,501,632$ (~345M parameters. The calculation is bigger than stated by OpenAI, like the author of the post said.)

Activation #

The paper ¹ mostly focus on reducing memory usage of activation. I borrow their analysis here (page 4).

Unlike model parameters, activation is proportional to the number of microbatch ($b$).

Their activation analysis is per layer. Need to multiply by $L$.

Their calculation is to get the amount of memory usage in bytes. For mask elements, only a byte per element is required, while others activations are stored in FP16 (2 bytes per element).

(1) for attention

Q, K, and V matrix multiplies: only need to store shared input $2sbh$.
$QK^T$ matrix multiply: requires stotage of both Q and K with total size $4sbh$.
Softmax: softmax output with size $2as^2b$ is required for back-propagation.
Softmax dropout: only a mask with size $as^2b$ is needed. (Note that they stated only a single byte per element is required for mask).
Attention over Values: need to store the dropout output ($2as^2b$) and V ($2sbh$).
Post-atention linear and dropout: required to store activations ($2sbh$ and $sbh$, respectively).

(2) for MLP

Linear, GeLU, and Dropout: Two linear layers and GeLU non-linarlity needs their inputs with $2sbh, 8sbh, 8sbh$, respectively, for back-propagation. dropout stores its mask with size $sbh$. Total: $19sbh$

(3) for Layer Norm: each layer norm stores its input with size $2sbh$ (total: $4sbh$).

Activation memory per layer: $sbh(34+5\frac{as}{h})$ or $34sbh+5as^2b$

For instance, GPT-2 medium with 8 microbatches: $1024 * 8 * 1024 * (34 + 5 * \frac{16 * 1024}{1024})$ = 912MB per layer. Considering that the entire model would only take 676MB, activation memory is so huge.

Gradient and Optimizer State #

Gradient is stored in FP16 as well, but the optimizer keeps an FP32 copy of the parameters and FP32 copy of all the other optimizer states, according to ZeRO ⁴.

The dimension of gradients is the same with that of the corresponding parameters. Hence, $12h^2$ per layer, or $12Lh^2+vh+sh$ for the entire model.

For optimizer state, Adam, for example, holds an FP32 copy of the parameters, momentum, and variance (assuming the number of parameter is $P$, memory requirement is $4P, 4P, 4P$, respectively).

Total gradient memory consumption: $2 * (12Lh^2 + (s+v)h)$, and for optimizer state: $12 * (12Lh^2 + (s+v)h)$.

For instance, GPT-2 medium: 709,003,264 bytes (676MB) for gradient, 4,254,019,584 bytes (3.96GB) for optimizer state.

Total Memory Consumption #

If not considering activation recomputation, peak memory consumption for GPT-2 medium with 8 microbatch would be roughly:

676MB (model parameters) + 21.375GB (activation) + 676MB (gradient) + 3.96GB (optimizer state) ~= 26.66GB

node00               Sun Jul 31 06:44:34 2022  510.60.02
[0] NVIDIA A40       | 36'C,   0 % | 29621 / 46068 MB |

Note that actual running includes more parameters (biases), input data, kernel, internal fragmented allocated but unused buffer, etc. Tested with Megatron-LM code (FP16, Adam, 8 microbatch size, GPT-2 medium).

Layer Dimension #

Model input: [$s, v, b$]. Multiplied by word embedding ([$v, h$]) (and add the position encoding [$s, h$]) to create a transformer layer input [$s, h, b$].
Transformer layer input: [$s, h, b$].
Q, K, and V: layer input [$s, h, b$] multiplied by weight [$h, h$] for each batch, respectively. each has [$s, h, b$]. Note that they are broken down to $a$ Q, K, and Vs, each of which has [$s, \frac{h}{a}, b$] ($\frac{h}{a}$ is called a query size and always 64 for all GPT-2 configuration).
In self-attention, $QK^T$ has [$s, s, b$]. There are $a$ $QK^T$, so in total number of elements is $as^2b$.
Softmax and dropout do not change dimension; same to that of $QK^T$: [$s, s, b$].
The dimension of the attention output after multiplying V ([$s, h, b$]) on $softmax(QK^T)$ ($[s, s, b]$) is [$s, h, b$].
Post attention linear projection multiplies its weight [$h, h, b$] without dimension change; the output dimension is [$s, h, b$].
In MLP, linear projection casts the hidden size of the self attention output from $h$ to $4h$ by multiplying its weight of [$h, 4h, b$]. The output dimension is [$s, 4h, b$].
GeLU is a element-wise operation, so the same with the input: [$s, 4h, b$].
The next linear reduces the input height from $4h$ to $h$ by multiplying its weight of [$4h, h, b$]. The output dimension is [$s, h, b$].
Layer normalization does not change the dimension, which makes the layer output dimension of [$s, h, b$].

FLOPs for Computing #

The paper for activation optimization ¹ also analyzed FLOPs calculation in Appendix A. Following their analysis, I also only consider the matrix multiplications (GEMMs: General Matrix Multiply).

I don’t know why, but the paper authors ¹ multiply every number of operations by 2. Here my calculations are half of theirs.

(1) for the attention block, main contributors to operations are:

key, query, and value transformation: $3sbh^2$ ([$s, h$] * [$h, h$] * b each)
attention matrix computation ($\frac{QK^T}{\sqrt{d_k}}$): $s^2hb$ ([$s, \frac{h}{a}$] * [$\frac{h}{a}, s$] * b per attention head, and there are $a$ heads)
attention over values (multiply attention matrix by V to calculate $attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$): $s^2bh$ ([$s, s$] * [$s, \frac{h}{a}$] * b per attention head, and there are $a$ heads)
post-attention linear projection: $sbh^2$ ([$s, h$] * [$h, h$] * b. Note that post-attention linear projection is done after concatenating $a$ attention heads into a single matrix of [$s, h$])

Total computation in attention: $4sbh^2 + 2s^2bh$

(2) for MLP (feed-forward):

linear projection casting hidden size $h$ to $4h$ and back to $h$: $8sbh^2$ ([$s, h$] * [$h, 4h$] * b and [$s, 4h$] * [$4h, h$] * b)

For each transformer layer with (1)+(2): $12sbh^2+2s^2bh$ for forward pass, and double the number of FLOPs for back-propagation (to calculate the gradients with respect to both input and weight tensors).

Total FLOPs per layer: $3b*(12sh^2+2s^2h)$.

For instance, GPT-2 medium with 8 microbatches: 3 * 8 * 15,032,385,536 = 360,777,252,864 FLOPs (336 GFLOPs) per layer per iteration. Considering the theoretical peak performance for a NVIDIA A40 GPU is 37.42 TFLOPS/s (non-tensor cores. Note peak fp16 tensor flops for A40 is 149.7 TFLOPS/s [datasheet]), executing FP+BP for 24 layers in GPT-2 medium would take ~210ms. Of course, actual computing requires data copy across memory hierarcy, and peak performance cannot be achieved because tensor cores are not always used, CUDA kernel launch delay, data transfer, etc. Actual performance in the test system shows:

iteration      100/     100 | consumed samples:          800 | elapsed time per iteration (ms): 646.3
time (ms) | forward-compute: 255.92 | backward-compute: 280.90 | ...