Backgrounds #

Attention #

$$\text{Attention}(Q, K, V)=\text{softmax}(\frac{QK^T}{\sqrt{d^k}})V$$

This equation can be implemented as:

class OPTAttention(nn.Module):
    def forward(...):
        # hidden states is an input tenor of Attention layer
        # Calculate Q, K, and V with linear projections to the input
        # query_states = self.q_proj(hidden_states)
        # key_states = self.k_proj(hidden_states)
        # value_states = self.v_proj(hidden_states)

        # QK^T
        attn_weights = torch.bmm(query_states, key_states.transpose(1, 2))

        # apply mask if exists

        # softmax
        attn_weights = nn.functional.softmax(attn_weights, ...)

        # dropout
        attn_probs = nn.functional.dropout(attn_weights, ...)

        # multiply by V
        attn_output = torch.bmm(attn_probs, value_states)

        ...

        # final linear. Depend on the model
        # attn_output = self.out_proj(attn_output)

which includes at least 4 CUDA kernel launches (bmm, softmax, dropout, bmm). Flash attention observed that for every kernel launch ouput results are written back to the GPU memory to make it addressable, and some operations are memory-intensive (softmax, dropout, and optionally mask). If results are written back to the global memory, it should be loaded back to SRAMs for computations, and if an operation is memory-intensive which cannot be hidden in computation, it is going slow.

See Section 2¹ to understand performance characteristics. Examples of compute-bound and memory-bound operations from the paper:

Compute-bound: Matrix multiply with large inner dimension, and convolution with large number of channels.

Memory-bound: elementwise (e.g. activation, dropout) and reduction (sum, softmax, batch norm, and layer norm).

If we fuse the operations (because what we need is an output of attention, not the result of each operation), intermediate results don’t have to be written back to the global memory, thus can be accelerated. I am rewriting paper’s algorithms in my terms.

Standard attention implementation (Section 2.2 of ¹) #

With Q ($[N \times d]$), K ($[N \times d]$), V ($[N \times d]$) matrices,

Read $Q$ and $K$ from global memory, compute $S=QK^T$ (flops: $N \times d \times N$), write $S ([N \times N])$ to global memory
Read $S$ from global memory, compute $P=\text{softmax}(S)$ (flops: $N \times N$), and write $P ([N \times N])$ to global memory. When calculating softmax, $A$ is temporarily assigned to store $exp(S)$.
Load $P$ and $V$ from global memory, compute $O=PV$ (flops: $N \times N \times d$), and write $O ([N \times d])$ to global memory.
Return $O$.

where $y=\text{softmax}(x)$ is defined as the following code:

import numpy as np

def softmax(x: np.array):
    e_x = np.exp(x)
    return e_x / np.sum(e_x, axis=0)

# Or safe-softmax with online normalizer:
def safe_softmax(x: np.array):
    m = np.max(x)
    e_x = np.exp(x - m)
    return e_x / np.sum(e_x, axis=0)

which rescales the tensor so that the elements of the n-dimensional output tensor lie in the range of [0, 1] and sum to 1.

Online Softmax ⁶ #

Because calculaing e_x relies on the maximum of x m, this cannot be done with calculation of m. Online softmax, instead, calculates the maximum value m online so that they can be fused and done in the same iteration. Later it is scaled back to calculat the correct value. For this lazy scaling, the algorithm keeps the maximum value m and the normalization term d:

def online_softmax(x: np.array):
    m: list[float] = [-math.inf] * (len(x) + 1)
    d: list[float] = [0] * (len(x) + 1)

    for i in range(len(x)):
        m[i + 1] = max(m[i], x[i])
        d[i + 1] = d[i] * e ** (m[i] - mi) + e ** (x[i] - mi)

    # m[-1] is the maximum value m, and d[-1] is the normalization term D^V. Scale the result back to get the correct value
    return [e ** (x[i] - m[-1]) / d[-1] for i in range(len(x))]

FlashAttention #

The main idea is to split Q, K, V into blocks, load them from slow global memory to fast SRAM, then compute the partial attention within a fused operation.

Note that FlashAttention and FlashAttention-2 have difference iteration. FlashAttention iterates Q in inner loope and K/V in outer loop, but in FlashAttention-2 iterates Q in outer loop and K/V in inner loop.

All illustrations are FlashAttention-2 base.

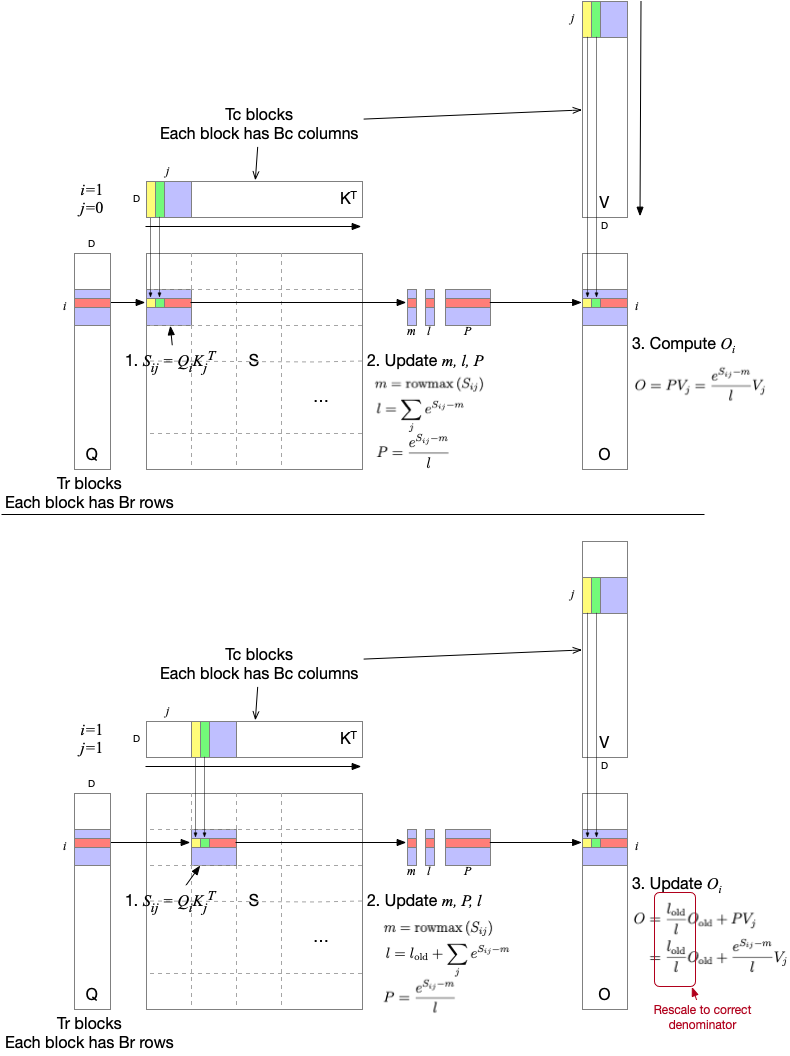
In inner loop of FlashAttention (line 3 to 11), it iterates K/V blocks and calculate attention for queries in a Qi block. Figure, for example, illustrates two inner-loop iterations with the second Q block (Q1). In the first subfigure (above), $P$ is attention score but calculated with local sum ($l$), which is not correct sum that is supposed to consider all keys. At this moment we don’t know what the global sum, we anyway use it (online softmax!).

In the second subfigure (below), when we update $O$, old $O$ value is rescaled with a newly updated local sum. $P$ here is calculated using all scores in two blocks that have been visited so far: $\frac{l_{\text{old}}}{l}O_{\text{old}}$ is equal to $\frac{l_{\text{old}}}{l} \frac{e^{S_{10}-m}}{l_{\text{old}}}V_0$, meaning the partial output is rescaled and aggregated.

By continuing this iterations, $P$ will eventually be correct score and previously calculated outputs will be added after rescaling.

FlashDecoding #

Because a single SM in a GPU does all iterations, FlashAttention underutilizes the GPU in inference if batch size is low, because there will be only 1 query token. Therefore, FlashDecoding partitions Key and Value matrices into multiple chunks and parallelize it.